Tree (BST) məlumat strukturu
-
2025 M03 27 13:16 üzərində yazmışdı sonuncu dəfə tərəfindən redaktə edilib
Ağac (Tree) verilənlər strukturu iyerarxik düyünlər (nodes) kolleksiyasıdır. Hər bir düyünün bir dəyəri olur və sıfır və ya daha çox alt düyünlərə (child nodes) sahib ola bilər. Ağaclar fayl sistemlərində, təşkilati diaqramlarda, verilənlərin axtarışı və sıralanması kimi sahələrdə geniş istifadə olunur. Ağacın yuxarı hissəsində kök (root) düyünü yerləşir, ondan aşağıya doğru budaqlanan düyünlər isə ən aşağı səviyyədə yarpaq (leaf) düyünləri ilə tamamlanır.
Ağac Terminologiyası
- Kök (Root) - Ağacın ən üst düyünü;
- Uşaq (Child) - Birbaşa başqa bir düyünə bağlı olan düyün;
- Valideyn (Parent) - Uşaq düyününə birbaşa bağlı olan düyün;
- Bacı-qardaş (Siblings) - Eyni valideynə sahib olan düyünlər;
- Yarpaq (Leaf) - Uşaq düyünü olmayan düyün;
- Kənar (Edge) - İki düyün arasındakı əlaqə.
İkili axtarış ağacı (BST) necə işləyir?
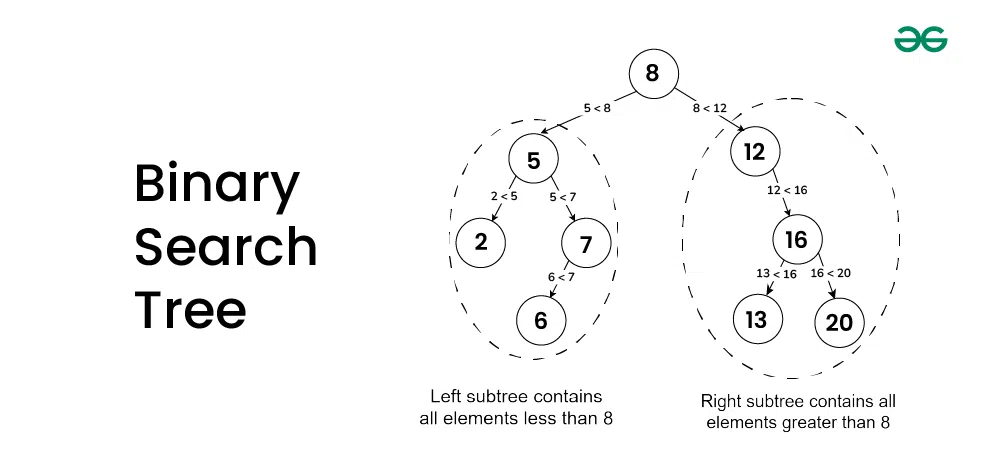
İkili axtarış ağacı (Binary Search Tree, BST) xüsusi bir ağac növüdür. Burada:
- Hər bir valideyn düyünü maksimum iki uşaq düyünə sahib ola bilər;
- Sol tərəfdəki bütün düyünlər həmişə valideyn düyünündən kiçik olur;
- Sağ tərəfdəki bütün düyünlər həmişə valideyn düyünündən böyük olur.
Bu struktur məlumatların səmərəli axtarışı və idarə olunması üçün idealdır.
BST-in implementasiyası
1. Əsas classın yaradılması
BST yaratmaq üçün aşağıdakı addımları yerinə yetiririk:
- BinarySearchTree adlı class yaradılır və constructor-da
this.root = nulltəyin olunur. - Node adlı class yaradılır. Bu class:
valueparametrini qəbul edir vəthis.value-a təyin edir;this.leftvəthis.rightsahələrinullolaraq başlayır.
2. Düyünün ağaca əlavə edilməsi (Insert metodu)
BST-də yeni düyün əlavə etmək üçün:
- Yeni düyün yaradılır.
- Əgər ağac boşdursa, yeni düyün
rootolur. - Əgər
rootvarsa:- Əgər yeni düyünün dəyəri
root-dan kiçikdirsə, sol tərəfə yerləşdirilir. - Əgər
root-dan böyükdürsə, sağ tərəfə yerləşdirilir.
- Əgər yeni düyünün dəyəri
- Əgər uyğun mövqe tapılmazsa, düyün rekursiv şəkildə yerləşdirilir.
Kod nümunəsi:
insert(value) { const newNode = new Node(value); if (!this.root) { this.root = newNode; return this; } let current = this.root; while (true) { if (value === current.value) return undefined; const direction = value < current.value ? 'left' : 'right'; if (!current[direction]) { current[direction] = newNode; return this; } else { current = current[direction]; } } }
3. Axtarış funksiyası (Find metodu)
Düyünün ağacda olub-olmadığını yoxlamaq üçün:
rootyoxlanılır. Əgərrootboşdursa, axtarış dayandırılır.- Əgər
root-un dəyəri axtarılan dəyərə bərabərdirsə, düyün tapıldı. - Əgər axtarılan dəyər
root-dan kiçikdirsə, sol budaqda axtarış davam edir. - Əgər axtarılan dəyər
root-dan böyükdürsə, sağ budaqda axtarış davam edir.
Kod nümunəsi:
find(value) { if (!this.root) return false; let current = this.root; while (current) { if (value < current.value) { current = current.left; } else if (value > current.value) { current = current.right; } else { return current; } } return false; }
İkili Ağacda axtarış alqoritmləri
Ağaclarda iki əsas axtarış metodu var:
- BFS (Eninə Axtarış - Breadth-First Search)
- DFS (Dərinliyə Axtarış - Depth-First Search)
1. BFS (Breadth-First Search) – Eninə Axtarış
BFS metodunda axtarış səviyyə-səviyyə aparılır:
- Queue strukturu yaradılır.
- Kök düyünü queue-yə əlavə edilir.
- Queue boş olmadığı müddətcə:
- Queue-dən düyün çıxarılır.
- Onun sol və sağ düyünləri queue-yə əlavə edilir.
- Axtarış başa çatır və nəticə qaytarılır.
Kod nümunəsi:
BFS() { let node = this.root, data = [], queue = []; queue.push(node); while (queue.length) { node = queue.shift(); data.push(node.value); if (node.left) queue.push(node.left); if (node.right) queue.push(node.right); } return data; }
2. DFS (Depth-First Search) – Dərinliyə Axtarış
DFS metodunda budaqlar tam araşdırılır və sonra geri qayıdılır.
DFS PreOrder (Öncə Valideyn, Sonra Uşaqlar)
- Kök düyün
datamassivinə əlavə edilir. - Sol alt ağac ziyarət olunur.
- Sağ alt ağac ziyarət olunur.
DFSPreOrder(){ const data = []; function traverse(node){ data.push(node.value); if(node.left) traverse(node.left); if(node.right) traverse(node.right); } traverse(this.root); return data; }
DFS PostOrder (Öncə uşaqlar, Sonra valideyn)
- Sol alt ağac ziyarət olunur.
- Sağ alt ağac ziyarət olunur.
- Valideyn düyün
datamassivinə əlavə edilir.
DFSPostOrder(){ var data = []; function traverse(node){ if(node.left) traverse(node.left); if(node.right) traverse(node.right); data.push(node.value); } traverse(this.root); return data; }
DFS InOrder (Sol -> Valideyn -> Sağ)
- Sol alt ağac ziyarət olunur.
- Valideyn düyün
datamassivinə əlavə edilir. - Sağ alt ağac ziyarət olunur.
DFSInOrder(){ var data = []; function traverse(node){ if(node.left) traverse(node.left); data.push(node.value); if(node.right) traverse(node.right); } traverse(this.root); return data; }
Bu məqalədə İkili Axtarış Ağacı (BST) və onun əsas axtarış alqoritmləri haqqında məlumat verdik. BST verilənlərin səmərəli idarə olunması və axtarışı üçün ideal bir strukturdur.

Bilik paylaşdıqca artan bir sərvətdir