Radix Sort-un Java proqramlaşdırma dilində implementasiyası

import java.util.ArrayList;
import java.util.List;

public class RadixSort {

    // Ədədin müəyyən mövqedəki rəqəmini qaytarır
    public static int getDigit(int num, int place) {
        return (int)(Math.abs(num) / Math.pow(10, place)) % 10;
    }

    // Ədədin neçə rəqəmdən ibarət olduğunu tapır
    public static int digitCount(int num) {
        if (num == 0) return 1;
        return (int)Math.floor(Math.log10(Math.abs(num))) + 1;
    }

    // Massivdə ən çox rəqəmə sahib ədədin rəqəm sayını tapır
    public static int mostDigits(int[] nums) {
        int maxDigits = 0;
        for (int num : nums) {
            maxDigits = Math.max(maxDigits, digitCount(num));
        }
        return maxDigits;
    }

    // Radix Sort-un əsas funksiyası
    public static int[] radixSort(int[] nums) {
        int maxDigitCount = mostDigits(nums);

        for (int k = 0; k < maxDigitCount; k++) {
            List<List<Integer>> digitBuckets = new ArrayList<>();

            // 0-dan 9-a qədər 10 bucket (siyahı) yaradılır
            for (int i = 0; i < 10; i++) {
                digitBuckets.add(new ArrayList<>());
            }

            // Ədədlər müvafiq bucket-lərə yerləşdirilir
            for (int num : nums) {
                int digit = getDigit(num, k);
                digitBuckets.get(digit).add(num);
            }

            // Bütün bucket-lər birləşdirilərək yeni massiv yaradılır
            int index = 0;
            for (List<Integer> bucket : digitBuckets) {
                for (int num : bucket) {
                    nums[index++] = num;
                }
            }
        }

        return nums;
    }

    // Test məqsədli əsas metod
    public static void main(String[] args) {
        int[] data = {170, 45, 75, 90, 802, 24, 2, 66};
        int[] sorted = radixSort(data);

        for (int num : sorted) {
            System.out.print(num + " ");
        }
    }
}

Nəticə:

2 24 45 66 75 90 170 802

Radix Sort — müqayisəyə əsaslanmayan (non-comparative) sıralama alqoritmidir. Bu alqoritm elementləri rəqəmlərinə (yəni rəqəm mövqelərinə) görə bucket adlı qruplara bölərək işləyir. Əməliyyat ya ən az əhəmiyyətli rəqəmdən (LSD - least significant digit) başlayaraq, ya da ən çox əhəmiyyətli rəqəmdən (MSD - most significant digit) başlayaraq aparılır. Bu proses, bütün rəqəmlər nəzərə alınana qədər davam edir.

Radix Sort, xüsusilə tam ədədlərin sıralanmasında effektivdir və O(nk) (k = ən böyük rəqəm sayı) kimi xətti zaman mürəkkəbliyinə malikdir. Bu, onu böyük verilənlər üçün ənənəvi müqayisəyə əsaslanan sıralama alqoritmlərindən daha sürətli edir. Lakin bu alqoritm üçün bütün ədədlərin eyni sayda rəqəmə sahib olması və ya bərabərləşdirilməsi vacibdir.

İmplementasiya

getDigit - Verilmiş ədədin istənilən rəqəmini almaq

Bu funksiya num ədədinin i-ci mövqedəki rəqəmini qaytarır:

const getDigit = (number, i) => {
  return Math.floor(Math.abs(number) / Math.pow(10, i)) % 10;
}

digitCount - Ədədin neçə rəqəmdən ibarət olduğunu qaytarmaq

Bu funksiya ədədin neçə rəqəmdən ibarət olduğunu tapır:

const digitCount = (number) => {
  return Math.floor(Math.log10(Math.abs(number))) + 1;
}

mostDigits - Massivdə ən çox rəqəmə sahib ədədin rəqəm sayını tapmaq

Bu funksiya bir massivdəki ən böyük rəqəm sayını tapır:

const mostDigits = (numberArray) => {
  let max = 0;
  for (let i = 0; i < numberArray.length; i++) {
    max = Math.max(max, digitCount(numberArray[i]));
  }
  return max;
}

Radix Sort-un özünün tətbiqi

1. Bir massiv qəbul edən radixSort funksiyasını yaradın;
2. Ən böyük ədədin neçə rəqəmə sahib olduğunu mostDigits funksiyası ilə tapın;
3. k = 0-dan başlayaraq bu ən böyük rəqəm sayına qədər dövr yaradın;
4. Hər iterasiyada:
   • digitBuckets adlı 0-dan 9-a qədər 10 boş qutu yaradın;
   • Ədədləri k-cı rəqəmlərinə görə uyğun qutulara yerləşdirin;
5. Massivi bucket-lərdəki dəyərlərlə yenidən qurun ([].concat(...digitBuckets));
6. Sonda sıralanmış massivi qaytarın;

Tam Həll:

const radixSort = (array) => {
  const largest = mostDigits(array);

  for (let k = 0; k < largest; k++) {
    const digitBuckets = Array.from({ length: 10 }, () => []);
    
    for (let i = 0; i < array.length; i++) {
      const digit = getDigit(array[i], k);
      digitBuckets[digit].push(array[i]);
    }

    array = [].concat(...digitBuckets);
  }

  return array;
}

Nəticə

Radix Sort — sadə, amma güclü bir alqoritmdir. Xüsusilə tam ədədlərlə işləyən və böyük verilənlərdə performans tələb edən sistemlərdə çox istifadə olunur. Əgər ədədlər eyni uzunluqda deyilsə, 0 ilə doldurularaq eyni uzunluğa gətirilə bilər. Radix Sort-un müqayisəyə əsaslanan sort alqoritmlərindən fərqli olaraq rəqəm əsaslı olması onu unikal və fərqli edir.

Quick Sort — sürətli, yerində (in-place) və müqayisəyə əsaslanan sıralama alqoritmidir. Bu alqoritm “pivot” adlanan bir element seçir və digər elementləri bu pivotdan kiçik və ya böyük olmalarına görə iki alt massivə ayırır. Daha sonra bu alt massivlər rekursiv şəkildə sıralanır. Quick Sort-un orta və ən yaxşı halda zaman mürəkkəbliyi O(n log n) olsa da, ən pis halda bu O(n²)-ə qədər arta bilər. Bununla belə, böyük verilənlər üzərində effektiv işlədiyinə görə çox istifadə olunur.

İmplementasiya

Pivot (partition) yardımçı funksiyası

1. Üç parametr qəbul edən bir funksiya yaradın: array, start indeksi və end indeksi (bunlar susmaya görə 0 və array.length - 1 ola bilər);
2. Elementləri dəyişmək üçün ayrıca bir köməkçi funksiya (swap) yaradın;
3. Pivotu seçin (məsələn, arr[start] dəyəri);
4. Hal-hazırkı pivot indeksini ayrıca bir dəyişəndə saxlayın;
5. start + 1-dən end-ə qədər dövr edin:
   • Əgər cari element pivotdan kiçikdirsə, pivot indeksini bir vahid artırın və cari elementi həmin yeni pivot indeksindəki elementlə dəyişdirin;
6. Pivotu yerləşdiyi start indeksindən, pivot indeksinə dəyişin;
7. Pivot indeksini qaytarın;

Həll:

const pivot = (arr, start = 0, end = arr.length - 1) => {
  const swap = (arr, idx1, idx2) => 
    [arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]];

  let pivot = arr[start];
  let swapIdx = start;

  for (let i = start + 1; i <= end; i++) {
    if (pivot > arr[i]) swap(arr, ++swapIdx, i);
  }

  swap(arr, start, swapIdx);
  
  return swapIdx;
}

Quick Sort alqoritminin özü

1. Üç parametr qəbul edən əsas funksiya yaradın: massiv, left (susmaya görə 0) və right (array.length - 1);
2. Əgər left < right şərti doğrudursa:
   • Pivot funksiyasını çağırın və massivlə birlikdə left, right dəyərlərini ötürün;
   • Pivot funksiyası sizə yeni pivot indeksini qaytardıqdan sonra, rekursiv şəkildə:
     • Pivotun solundakı altmassiv üçün quickSort(arr, left, pivotIndex - 1)
     • Pivotun sağındakı altmassiv üçün quickSort(arr, pivotIndex + 1, right) çağırın;
3. Əks halda sadəcə massiv qaytarılır;

Həll:

const quickSort = (arr, left = 0, right = arr.length - 1) => {
  if (left < right) {
    const pivotIndex = pivot(arr, left, right);
    quickSort(arr, left, pivotIndex - 1);
    quickSort(arr, pivotIndex + 1, right);
  }

  return arr;
}

Nəticə

Quick Sort yüksək performans və minimal yaddaş istifadəsi ilə tanınır. Əgər düzgün seçilmiş pivot istifadə edilərsə, böyük verilənlər üçün olduqca effektiv olur. Lakin ən pis ssenaridə O(n²) mürəkkəbliyə malik olduğu üçün bəzən alternativ alqoritmlərlə müqayisə etmək lazımdır.

Quick Sort-u vizual olaraq görmək üçün Macar (Küküllőmenti legényes) xalq rəqsinə tamaşa etməniz kifayət edəcək

İkiölçülü massivlər (matrislər) Java proqramlaşdırma dilində məlumatların sətir və sütunlar şəklində təşkil edilməsi üçün istifadə olunan vacib məlumat strukturlarındandır. Bu məqalədə, Java-da ikiölçülü massivlərin nə olduğunu, necə elan edilib başlandığını və onlarla necə işləmək lazım olduğunu araşdıracağıq.

İkiölçülü massiv (matris) nədir?

İkiölçülü massivlər, sətir və sütunlardan ibarət olan və məlumatların cədvəl formasında saxlanmasına imkan verən massivlərdir. Məsələn, 4 sətir və 4 sütundan ibarət bir matris aşağıdakı kimi təsvir edilə bilər:

Java-da bu matris ikiölçülü massiv kimi təmsil edilə bilər. İkiölçülü massivlərdə ilk indeks sətiri, ikinci indeks isə sütunu göstərir. Məsələn, int[][] matrix = new int[4][4]; ifadəsi 4 sətir və 4 sütundan ibarət bir matris yaradır.

İkiölçülü massivin elan edilməsi və başlanğıc dəyər verilməsi

Java-da ikiölçülü massivləri müxtəlif yollarla elan edib başlanğıc dəyər vermək mümkündür:

public class Matrisler {
    public static void main(String[] args) {
        // 2x2 ölçülü tam ədəd massivinin elan edilməsi
        int[][] matris1 = new int[2][2];

        // 2x3 ölçülü tam ədəd massivinin elan edilməsi
        int[][] matris2 = new int[2][3];

        // 4x4 ölçülü massivə başlanğıc dəyərlərin verilməsi
        int[][] matris3 = {
            {3, 2, 1, 7},
            {9, 11, 5, 4},
            {6, 0, 13, 17},
            {7, 21, 14, 15}
        };

        // 2x2 ölçülü string massivinin elan edilməsi
        String[][] matris4 = new String[2][2];

        // Fərqli uzunluqlu sətirlərə malik massiv
        String[][] matris5 = {
            {"a", "lion", "meo"},
            {"jaguar", "hunt"}
        };
    }
}

Yuxarıdakı nümunələrdə müxtəlif ölçülərdə və tiplərdə ikiölçülü massivlərin necə elan edilib başlanğıc dəyər verildiyi göstərilir.

İkiölçülü massivin travers edilməsi (gəzinilməsi)

İkiölçülü massivlərdə məlumatlara daxil olmaq və onları işləmək üçün iç-içə (nested) for döngülərindən istifadə edilir. Aşağıdakı nümunədə 4x4 ölçülü bir matrisin sətir və sütunlarının indeksləri çap edilir:

public class MatrisTravers {
    public static void main(String[] args) {
        int[][] matris = new int[4][4];
        for (int i = 0; i < matris.length; i++) {
            System.out.print("sətir " + i + " : ");
            for (int j = 0; j < matris[i].length; j++) {
                System.out.print("sütun " + j + "  ");
            }
            System.out.println();
        }
    }
}

Bu proqramın çıxışı aşağıdakı kimi olacaq:

sətir 0 : sütun 0  sütun 1  sütun 2  sütun 3  
sətir 1 : sütun 0  sütun 1  sütun 2  sütun 3  
sətir 2 : sütun 0  sütun 1  sütun 2  sütun 3  
sətir 3 : sütun 0  sütun 1  sütun 2  sütun 3  

Burada matris.length sətirlərin sayını, matris[i].length isə hər sətirdəki sütunların sayını göstərir.

İkiölçülü massivin çap edilməsi

İkiölçülü massivdəki məlumatları çap etmək üçün iç-içə for döngələrindən istifadə olunur. Aşağıdakı nümunədə bir matrisin elementləri çap edilir:

public class MatrisCapi {
    public static void matrisCapi(int[][] matris) {
        for (int i = 0; i < matris.length; i++) {
            for (int j = 0; j < matris[i].length; j++) {
                System.out.print(matris[i][j] + "\t");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int[][] matris = {
            {3, 2, 1, 7},
            {9, 11, 5, 4},
            {6, 0, 13, 17},
            {7, 21, 14, 15}
        };
        matrisCapi(matris);
    }
}

Bu proqramın çıxışı aşağıdakı kimi olacaq:

3	2	1	7	
9	11	5	4	
6	0	13	17	
7	21	14	15	

Burada \t istifadə edərək elementlər arasında boşluq yaradılır ki, nəticə daha oxunaqlı olsun.

İkiölçülü massivlər Java proqramlaşdırma dilində məlumatların cədvəl formasında saxlanması və işlənməsi üçün güclü bir vasitədir. Onların düzgün elan edilməsi, başlanğıc dəyər verilməsi və gəzinilməsi proqramların effektivliyini artırır və kodun daha səliqəli olmasına kömək edir.

1.3.21 - Kary

Tapşırıq: İki tam ədəd (i və k) qəbul edən bir proqram yazın və i ədədini k əsasında konvert edin. k 2 ilə 16 arasında olmalıdır. Əgər əsas 10-dan böyükdürsə, 11-dən 16-ya qədər olan rəqəmləri A-F kimi göstərmək lazımdır.

Spoiler

public class Kary {
    public static void main(String[] args) {
        long i = Long.parseLong(args[0]);
        int k = Integer.parseInt(args[1]);

        String digits = "0123456789ABCDEF";
        StringBuilder result = new StringBuilder();

        while (i > 0) {
            int remainder = (int)(i % k);
            result.insert(0, digits.charAt(remainder));
            i /= k;
        }

        System.out.println(result.toString());
    }
}

1.3.28 - Factors dövrünün dayandırılma şərtinin təsiri

Tapşırıq: (factor < n) yerinə (factor <= n / factor) istifadə etdikdə proqramın performansına necə təsir etdiyini yoxlayın. 10 saniyə ərzində tamamlana biləcək ən böyük n tapın.

Spoiler

public class Factors {
    public static void main(String[] args) {
        long n = Long.parseLong(args[0]);
        for (long factor = 2; factor <= n / factor; factor++) {
            while (n % factor == 0) {
                System.out.print(factor + " ");
                n /= factor;
            }
        }
        if (n > 1) System.out.print(n);
    }
}

Qısa təhlil: Yeni şərt (factor <= n / factor) daha az iterasiya etməyə səbəb olur və böyük n üçün daha sürətlidir.

1.3.31 - Relatively Prime (Nisbətən sadə ədədlər cədvəli)

Tapşırıq: n daxil edin və n x n ölçülü cədvəl çap edin. Əgər i və j ədədlərinin ƏBOB-u 1-dirsə, həmin mövqedə * çap olunsun, əks halda boşluq ( ) qoyulsun.

Spoiler

public class RelativelyPrime {
    public static int gcd(int a, int b) {
        if (b == 0) return a;
        return gcd(b, a % b);
    }

    public static void main(String[] args) {
        int n = Integer.parseInt(args[0]);

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if (gcd(i, j) == 1) System.out.print("* ");
                else System.out.print("  ");
            }
            System.out.println();
        }
    }
}

1.3.34 - Ramanujan’ın taksi nömrəsi

Tapşırıq: a³ + b³ = c³ + d³ bərabərliyini ödəyən fərqli müsbət tam ədədləri (a, b, c, d) tapın ki, a³ + b³ bir ədəd olsun və bu ədəd eyni zamanda başqa iki ədədin kub cəmi kimi ifadə oluna bilsin.

Spoiler

public class Ramanujan {
    public static void main(String[] args) {
        int n = Integer.parseInt(args[0]);

        for (int a = 1; a <= n; a++) {
            for (int b = a + 1; b <= n; b++) {
                for (int c = 1; c <= n; c++) {
                    for (int d = c + 1; d <= n; d++) {
                        int sum1 = a*a*a + b*b*b;
                        int sum2 = c*c*c + d*d*d;

                        if (sum1 == sum2 && a != c && a != d && b != c && b != d) {
                            System.out.println(sum1 + " = " + a + "^3 + " + b + "^3 = " + c + "^3 + " + d + "^3");
                        }
                    }
                }
            }
        }
    }
}

1.3.36 - Sadə ədədlərin sayılması

Tapşırıq: n daxil edin və n-dən kiçik və ya bərabər olan sadə ədədlərin sayını tapın.

Spoiler

public class PrimeCounter {
    public static boolean isPrime(int n) {
        if (n < 2) return false;
        for (int i = 2; i*i <= n; i++) {
            if (n % i == 0) return false;
        }
        return true;
    }

    public static void main(String[] args) {
        int n = Integer.parseInt(args[0]);
        int count = 0;

        for (int i = 2; i <= n; i++) {
            if (isPrime(i)) count++;
        }

        System.out.println("Sadə ədədlərin sayı: " + count);
    }
}

1.3.37 - 2D Random Walk (Təsadüfi gəzinti)

Tapşırıq: n daxil edin. 2n x 2n kvadratın sərhədinə qədər təsadüfi gəzən bir hissəciyin neçə addıma çatacağını təxmin edən proqram yazın.

Spoiler

public class RandomWalker {
    public static void main(String[] args) {
        int n = Integer.parseInt(args[0]);
        int x = 0, y = 0;
        int steps = 0;

        while (Math.abs(x) < n && Math.abs(y) < n) {
            double r = Math.random();
            if (r < 0.25) x++;          // şərq
            else if (r < 0.5) x--;      // qərb
            else if (r < 0.75) y++;     // şimal
            else y--;                   // cənub
            steps++;
        }

        System.out.println("Addım sayı: " + steps);
    }
}

Merge Sort — çox effektiv və müqayisəyə əsaslanan sıralama alqoritmidir. Bu alqoritm sıralanmamış massivləri iki yerə bölərək rekursiv şəkildə sıralayır və daha sonra bu sıralanmış hissələri birləşdirərək tək bir sıralanmış massiv yaradır. Bu proses massiv tamamilə sıralanana qədər davam edir.

Merge Sort-un zaman mürəkkəbliyi O(n log n) təşkil edir ki, bu da onu böyük verilənlər üzərində işləmək üçün uyğun edir. Eyni zamanda stabil alqoritm hesab olunur, yəni sıralama zamanı eyni dəyərə sahib elementlərin əvvəlki ardıcıllığı qorunur.

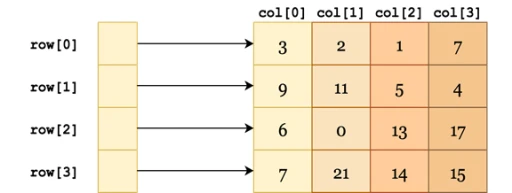
️ Merge Sort-un implementasiyası

İki massivin birləşdirilməsi funksiyası

İlk addım olaraq sıralanmış iki massiv birləşdirilir. Bu mərhələ, Merge Sort funksiyasının əsas tərkib hissəsidir.

1. Boş bir nəticə massivi yaradılır, hər iki massivin başlanğıcındakı ən kiçik dəyərlərə baxılır;
2. Massivlərdə hələ də baxılmamış dəyərlər olduqca:
   • Əgər birinci massivdəki dəyər ikincidəkindən kiçikdirsə, bu dəyər nəticə massivinə əlavə edilir və birinci massivdə növbəti dəyərə keçilir;
   • Əgər ikinci massivdəki dəyər birincidən kiçikdirsə, həmin dəyər əlavə olunur və ikinci massivdə növbəti dəyərə keçilir;
   • Əgər hansısa massiv bitibsə, digərindəki bütün dəyərlər əlavə olunur.

Kod nümunəsi:

const mergeArrays = (arr1: number[], arr2: number[]): number[] => {
  const result: number[] = [];
  let i = 0, j = 0;

  while (i < arr1.length || j < arr2.length) {
    if (arr2[j] === undefined || arr1[i] < arr2[j]) {
      result.push(arr1[i++]);
    } else {
      result.push(arr2[j++]);
    }
  }

  return result;
}

🧠 Merge Sort alqoritminin özünü

1. Əgər massivdə 1 və ya 0 element varsa, o artıq sıralanmış sayılır və olduğu kimi qaytarılır;
2. Massiv ortadan ikiyə bölünür. Bunun üçün mid dəyişəni yaradılır və Math.floor(array.length / 2) ilə təyin olunur;
3. Sonra left və right adlı iki massiv yaradılır. Bunlar slice() funksiyası ilə massivdən ayrılır:
   • left → array.slice(0, mid)
   • right → array.slice(mid)
4. left və right massivləri mergeSort funksiyası ilə rekursiv şəkildə sıralanır;
5. Sonda mergeArrays(left, right) funksiyası ilə sıralanmış hissələr birləşdirilir və nəticə olaraq geri qaytarılır.

Kod nümunəsi:

const mergeSort = (array: number[]): number[] => {
  if (array.length <= 1) return array;

  const mid = Math.floor(array.length / 2);
  const left = mergeSort(array.slice(0, mid));
  const right = mergeSort(array.slice(mid));

  return mergeArrays(left, right);
}

Nəticə

Merge Sort — həm sabit, həm də optimal zaman mürəkkəbliyinə malik olan güclü sıralama alqoritmidir. Onun əsas üstünlükləri:

• Böyük verilənlər üçün uyğundur;
• Eyni elementlərin sırasını qoruyur (stabil sıralama);
• Rekursiv yanaşma və “böl və fəth et” paradiqminə əsaslanır;
• O(n log n) performansı ilə çox effektivdir.

Merge Sort-u vizual olaraq görmək üçün Transilvaniya-sakson (alman) xalq rəqsinə tamaşa etməniz kifayət edəcək

Doubly Linked List-in Typescript-də full implementasiyası

// Node classı
class Node<T> {
  value: T; // Dəyər
  next: Node<T> | null; // Növbəti qovşağa işarə
  prev: Node<T> | null; // Əvvəlki qovşağa işarə

  constructor(value: T) {
    this.value = value;
    this.next = null;
    this.prev = null;
  }
}

// DLL classı
class DoublyLinkedList<T> {
  head: Node<T> | null; // Baş qovşaq
  tail: Node<T> | null; // Sonuncu qovşaq
  length: number; // Siyahının uzunluğu

  constructor() {
    this.head = null;
    this.tail = null;
    this.length = 0;
  }

  // Siyahının sonuna element əlavə etmək
  push(value: T): this {
    const newNode = new Node(value);
    if (!this.head) {
      // Siyahı boşdursa, həm head, həm tail eyni node olur
      this.head = newNode;
    } else {
      if (this.tail) {
        this.tail.next = newNode;
        newNode.prev = this.tail;
      }
    }
    this.tail = newNode;
    this.length++;
    return this;
  }

  // Siyahının sonundan element silmək
  pop(): Node<T> | undefined {
    if (!this.head) return undefined;

    const removed = this.tail!;
    if (this.length === 1) {
      // Siyahıda tək element varsa, hər ikisi də `null` olur
      this.head = null;
      this.tail = null;
    } else {
      this.tail = removed.prev;
      if (this.tail) this.tail.next = null;
      removed.prev = null;
    }
    this.length--;
    return removed;
  }

  // Siyahının əvvəlindən element silmək
  shift(): Node<T> | undefined {
    if (!this.head) return undefined;

    const removed = this.head;
    if (this.length === 1) {
      this.head = null;
      this.tail = null;
    } else {
      this.head = removed.next;
      if (this.head) this.head.prev = null;
      removed.next = null;
    }
    this.length--;
    return removed;
  }

  // Siyahının əvvəlinə element əlavə etmək
  unshift(value: T): this {
    const newNode = new Node(value);
    if (!this.head) {
      this.head = newNode;
      this.tail = newNode;
    } else {
      this.head.prev = newNode;
      newNode.next = this.head;
      this.head = newNode;
    }
    this.length++;
    return this;
  }

  // Verilmiş indeksə əsasən qovşağı əldə etmək
  get(index: number): Node<T> | null {
    if (index < 0 || index >= this.length) return null;

    let current: Node<T>;
    let count: number;

    // İndeks siyahının ortasından əvvəldirsə, başdan axtar
    if (index <= this.length / 2) {
      current = this.head!;
      count = 0;
      while (count !== index) {
        current = current.next!;
        count++;
      }
    } else {
      // Ortanı keçibsə, sondan axtar
      current = this.tail!;
      count = this.length - 1;
      while (count !== index) {
        current = current.prev!;
        count--;
      }
    }

    return current;
  }

  // Verilmiş indeksdəki qovşağın dəyərini dəyişmək
  set(index: number, value: T): boolean {
    const node = this.get(index);
    if (node) {
      node.value = value;
      return true;
    }
    return false;
  }

  // Verilmiş indeksə yeni qovşaq əlavə etmək
  insert(index: number, value: T): boolean {
    if (index < 0 || index > this.length) return false;
    if (index === 0) return !!this.unshift(value);
    if (index === this.length) return !!this.push(value);

    const newNode = new Node(value);
    const before = this.get(index - 1);
    const after = before!.next;

    before!.next = newNode;
    newNode.prev = before;
    newNode.next = after;
    if (after) after.prev = newNode;

    this.length++;
    return true;
  }

  // Verilmiş indeksdəki qovşağı silmək
  remove(index: number): Node<T> | undefined {
    if (index < 0 || index >= this.length) return undefined;
    if (index === 0) return this.shift();
    if (index === this.length - 1) return this.pop();

    const removed = this.get(index)!;
    const before = removed.prev!;
    const after = removed.next!;

    before.next = after;
    after.prev = before;

    removed.next = null;
    removed.prev = null;

    this.length--;
    return removed;
  }

  // Siyahını array kimi qaytarmaq (debug üçün)
  toArray(): T[] {
    const result: T[] = [];
    let current = this.head;
    while (current) {
      result.push(current.value);
      current = current.next;
    }
    return result;
  }
}

Jenny “bajı” qəşşəng başa salır. Baxmağa dəyər

İki istiqamətli bağlı siyahı (DLL) — hər bir elementi həm özündən əvvəlki, həm də özündən sonrakı elementə işarə edən iki göstərici ilə saxlayan xüsusi bir bağlı siyahı növüdür. Bu struktur elementlər arasında irəli və geri hərəkət etməyə imkan verir.

DLL, verilənlərin həm irəli, həm də geri istiqamətdə rahat idarə olunması üçün istifadə olunur.

DLL İstifadə Sahələri:

1. Mətn redaktorları – hər bir sətri node kimi saxlamaq və kursorla irəli-geri hərəkət etmək.
2. Undo/Redo funksionallığı – dizayn proqramlarında istifadə olunur.
3. Musiqi siyahıları – musiqilər arasında irəli və geri keçid.
4. Brauzer tarixi – əvvəlki və növbəti səhifələrə keçid.
5. Cache idarəsi – yaddaşda tez-tez istifadə olunan elementləri önə çəkmək.
6. Tapşırıq idarəetməsi – tapşırıqları asanlıqla əlavə/çıxarmaq və dəyişdirmək.
7. Verilənlər bazası idarəçiliyi – tranzaksiyaları izləmək və idarə etmək.
8. Real-time sistemlər – sabit və səmərəli yaddaş ayırması üçün.
9. Dinamik məlumat strukturları – deque, queue və s. üçün əsas struktur.

Tətbiq – JavaScript ilə DLL qurulması

Node və DoublyLinkedList classları

class Node {
  constructor(value) {
    this.value = value;
    this.next = null;
    this.prev = null;
  }
}

class DoublyLinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
    this.length = 0;
  }

push(value) – Siyahının sonuna əlavə etmə (O(1))

push(value) {
  const newNode = new Node(value);

  if (!this.length) {
    this.head = newNode;
  } else {
    this.tail.next = newNode;
    newNode.prev = this.tail;
  }

  this.tail = newNode;
  this.length++;

  return this;
}

pop() – Siyahının sonundan element silmək (O(1))

pop() {
  if (!this.head) return undefined;

  const current = this.tail;

  if (this.length === 1) {
    this.head = null;
    this.tail = null;
  } else {
    this.tail = current.prev;
    this.tail.next = null;
    current.prev = null;
  }

  this.length--;
  return current;
}

shift() – Siyahının əvvəlindən element silmək (O(1))

shift() {
  if (!this.length) return undefined;

  const current = this.head;

  if (this.length === 1) {
    this.head = null;
    this.tail = null;
  } else {
    this.head = current.next;
    this.head.prev = null;
    current.next = null;
  }

  this.length--;
  return current;
}

unshift(value) – Siyahının əvvəlinə element əlavə etmək (O(1))

unshift(value) {
  const newNode = new Node(value);

  if (!this.length) {
    this.head = newNode;
    this.tail = newNode;
  } else {
    this.head.prev = newNode;
    newNode.next = this.head;
    this.head = newNode;
  }

  this.length++;
  return this;
}

get(index) – İndeksə görə elementi əldə etmək (O(n))

get(index) {
  if (index < 0 || index >= this.length) return null;

  let count, current;

  if (index <= this.length / 2) {
    count = 0;
    current = this.head;
    while (count !== index) {
      current = current.next;
      count++;
    }
  } else {
    count = this.length - 1;
    current = this.tail;
    while (count !== index) {
      current = current.prev;
      count--;
    }
  }

  return current;
}

set(value, index) – İndeksə uyğun elementin dəyərini dəyişmək (O(n))

set(value, index) {
  const currentNode = this.get(index);
  if (currentNode) {
    currentNode.value = value;
    return true;
  }
  return false;
}

insert(value, index) – Müəyyən mövqeyə element əlavə etmək (O(n))

insert(value, index) {
  if (index < 0 || index > this.length) return false;
  if (index === 0) return this.unshift(value);
  if (index === this.length) return this.push(value);

  const newNode = new Node(value);
  const beforeNode = this.get(index - 1);
  const afterNode = beforeNode.next;

  beforeNode.next = newNode;
  newNode.prev = beforeNode;
  newNode.next = afterNode;
  afterNode.prev = newNode;

  this.length++;
  return true;
}

remove(index) – Müəyyən mövqedən elementi silmək (O(n))

remove(index) {
  if (index < 0 || index >= this.length) return false;
  if (index === 0) return this.shift();
  if (index === this.length - 1) return this.pop();

  const removedNode = this.get(index);
  removedNode.prev.next = removedNode.next;
  removedNode.next.prev = removedNode.prev;
  removedNode.next = null;
  removedNode.prev = null;

  this.length--;
  return removedNode;
}

🧠 Nəticə

Doubly Linked List – məlumatların idarəsini rahatlaşdıran və performans baxımından bir çox üstünlüyə sahib olan vacib məlumat strukturlarındandır. JavaScript-də bu strukturu sıfırdan qurmaq, həm nəzəri bilikləri praktikləşdirmək, həm də data strukturları sahəsində biliklərinizi möhkəmləndirmək üçün əla təcrübədir.

Maşın öyrənməsi (Machine Learning) süni intellektin ən vacib sahələrindən biridir və müxtəlif növ öyrənmə metodlarını əhatə edir. Nəzarətli maşın öyrənməsi (Supervised Learning) bu sahənin ən geniş yayılmış növüdür və real dünyada bir çox tətbiq sahəsinə malikdir. Bu yazıda nəzarətli öyrənmə, onun əsas növləri olan regressiya və klassifikasiya haqqında danışacağıq.

Nəzarətli maşın öyrənməsi nədir?

Nəzarətli maşın öyrənməsində model etiketlənmiş verilənlər üzərində öyrədilir. Yəni, hər giriş (Input) veriləninə uyğun bir çıxış (Output) dəyəri (etiket) mövcuddur. Modelin məqsədi bu verilənlərdən qaydaları öyrənərək gələcəkdə yeni verilənlər üçün düzgün proqnozlar verməkdir.

Məsələn, sizdə avtomobillərin ilinə və gündəlik istifadəsinə əsasən onların satış qiymətini göstərən verilənlər bazası varsa, nəzarətli maşın öyrənməsi modeli bu məlumatlardan istifadə edərək yeni avtomobillərin satış qiymətini proqnozlaşdıra bilər.

Nəzarətli öyrənmənin iki əsas növü

Nəzarətli öyrənmənin iki əsas növü var:

1. Regressiya (Regression) – Kəmiyyət (rəqəmsal) dəyərləri proqnozlaşdırmaq üçün istifadə olunur.
2. Klassifikasiya (Classification) – Məlumatları müəyyən kateqoriyalara ayırmaq üçün istifadə olunur.

Hər iki metod fərqli növ problemlərin həlli üçün istifadə olunur. İndi onların hər birini daha ətraflı araşdıraq.

Regressiya (Regression)

Regressiya modeli kəmiyyət (rəqəmsal) nəticələri proqnozlaşdırmaq üçün istifadə olunur. Başqa sözlə, bir və ya bir neçə dəyişənin təsiri ilə davamlı (continuous) bir dəyəri təxmin edirik.

Regressiyaya aid misallar:

• Ev qiymətlərinin proqnozlaşdırılması
• Hava temperaturunun proqnozlaşdırılması
• Müəssisənin gəlirinin təxmin edilməsi
• Avtomobilin yanacaq sərfiyyatının hesablanması

Regressiya modelləri arasında ən məşhurları:

• Xətti Regressiya (Linear Regression)
• Çoxlu Xətti Regressiya (Multiple Linear Regression)
• Lojistik Regressiya (Logistic Regression) - Klassifikasiya üçün də istifadə olunur

Xətti Regressiya (Linear Regression)

Xətti regressiya sadə və effektiv bir yanaşmadır. Burada model verilənlər arasındakı xətti münasibəti müəyyən edir. Məsələn, avtomobilin ili artdıqca onun qiymətinin azalması xətti bir münasibətdir.

Xətti regresiyanın ümumi tənliyi:

[y = mx + b]

Burada:

• ( y ) – proqnozlaşdırılan dəyərdir,
• ( m ) – dəyişənin təsir əmsalıdır,
• ( x ) – giriş dəyişənidir,
• ( b ) – sabit dəyərdir.

Məsələn, bir şirkət reklama xərclədiyi məbləğə əsasən satışlarını proqnozlaşdırmaq istəyirsə, xətti regresiya modelindən istifadə edə bilər.

Klassifikasiya (Classification)

Klassifikasiya modeli məlumatları fərqli kateqoriyalara ayırmaq üçün istifadə olunur. Yəni, nəticə diskret (categorical) dəyərdir.

Klassifikasiyaya aid misallar:

• Email-lərin “spam” və ya “normal” olaraq ayrılması
• Xəstənin müəyyən bir xəstəliyə malik olub-olmamasının təxmin edilməsi
• Şəkildə obyektin “pişik” və ya “it” olduğunu müəyyən etmək
• Müştərinin kredit ala bilib-bilməməsi haqqında qərar vermək

Lojistik Regressiya (Logistic Regression)

Adı regressiya olsa da, lojistik regressiya əslində klassifikasiya üçün istifadə olunur. Model, nəticəni 0 və 1 arasında ehtimalla proqnozlaşdırır və nəticəni müəyyən bir həddən (threshold) yuxarı və ya aşağı olaraq iki qrupa ayırır.

Lojistik funksiyanın tənliyi belədir:

[P(y) = \frac{1}{1 + e^{-z}}]

Burada:

• ( P(y) ) – bir hadisənin baş vermə ehtimalıdır,
• ( e ) – Eyler sabitidir (~2.718),
• ( z ) – giriş dəyişənlərinin xətti kombinasiyasıdır.

Əgər modelin proqnozlaşdırdığı ehtimal 0.5-dən böyükdürsə, model “1” (Məsələn, “spam”) nəticəsini verir, əks halda “0” (Məsələn, “normal email”) nəticəsi alınır.

Regressiya və Klassifikasiya Arasındakı Fərqlər

Nəticə

Nəzarətli maşın öyrənməsi süni intellektin ən fundamental sahələrindən biridir və iki əsas istiqaməti vardır: regressiya və klassifikasiya.

• Regressiya rəqəmsal qiymətləri proqnozlaşdırmaq üçün istifadə olunur.
• Klassifikasiya isə verilənləri müxtəlif kateqoriyalara ayırmaq üçün tətbiq edilir.

Bu metodlar maliyyə, səhiyyə, marketinq, mühəndislik və bir çox sahədə istifadə olunur və süni intellektin inkişafında böyük rol oynayır.

Java-da qlobal dəyişənlər tətbiqin istənilən yerindən əlçatan olan dəyişənlərdir. Bu dəyişənlərə bütün tətbiq boyunca müraciət etmək mümkündür. Qlobal dəyişən yaratmaq üçün public və static açar sözlərindən istifadə edilir:

public class Numune {
    public static int a;
    public static int b;
    public static String str;
}

Bu nümunədə a, b və str dəyişənləri qlobaldır və digər class-lardan birbaşa əlçatan olurlar:

public class QlobalDeyisenDemo {
    public static void main(String[] args) {
        Numune.a = 4;
        Numune.b = 5;
        Numune.str = "Qlobal String dəyişəninin dəyəri";

        System.out.println(Numune.a);
        System.out.println(Numune.b);
        System.out.println(Numune.str);
    }
}

Bu kodu icra etdikdə aşağıdakı nəticəni görəcəyik:

4
5
Qlobal String dəyişəninin dəyəri

Qlobal dəyişənlər iki növə bölünə bilər:

1. Dəyişdirilə bilən dəyişənlər.
2. Yalnız oxuna bilən dəyişənlər (qlobal sabitlər).

Qlobal sabit yaratmaq üçün dəyişəni final açar sözü ilə təyin edib, ona dəyər mənimsətmək lazımdır:

public class Sabitler {
    public static final double PI = 3.141592653589793;
    public static final String SALAM_DUNYA_STR = "Salam, Dünya!";
}

Java adlandırma konvensiyasına görə, bütün sabitlər böyük hərflərlə və sözlər arasında alt xətt (_) istifadə edilərək adlandırılmalıdır. Bu sabitlərin dəyərlərini dəyişmək mümkün deyil, lakin onları oxumaq mümkündür:

public class SalamDunya {
    public static void main(String[] args) {
        System.out.println(Sabitler.SALAM_DUNYA_STR);
    }
}

Nəticə:

Salam, Dünya!

Aşağıdakı nümunədə isə dairənin sahəsini hesablayan bir metod göstərilir:

public class SabitlerDemo {
    public static void main(String[] args) {
        double r = 10;
        String mesaj = String.format("Radiusu %f olan dairənin sahəsi=%f", r, daireSahesi(r));
        System.out.println(mesaj);
    }

    static double daireSahesi(double r) {
        return Sabitler.PI * r * r;
    }
}

Nəticə:

Radiusu 10.000000 olan dairənin sahəsi=314.159265

Qlobal dəyişənlərdən istifadə etməliyikmi?

İnternetdə qlobal dəyişənlərin istifadəsinin zərərli olduğunu bildirən çoxlu məqalələr mövcuddur. Gəlin, qlobal dəyişənlərin üstünlük və çatışmazlıqlarını nəzərdən keçirək ki, hər kəs öz nəticəsini çıxara bilsin.

Çatışmazlıqlar:

1. Kodun oxunaqlılığı azalır və başa düşülməsi çətinləşir.
2. Kodun saxlanması və dəstəklənməsi mürəkkəbləşir.
3. Bir qlobal dəyişəni dəyişdirmək üçün bütün kodu analiz etmək lazımdır.
4. Səhvlərin sayı artır və onları debug etmək çətinləşir.

Məsələn, bir qlobal dəyişən obyektlərdən ibarət bir massivdirsə, sistemin bir hissəsində bu massivdə sətirlər gözlənilir, digər hissəsində isə fərqli tipdə obyektlər ola bilər. Bu, uyğunsuzluqlara və səhvlərə səbəb ola bilər.

Üstünlüklər:

1. Bəzi hallarda qlobal dəyişənlər kodun strukturunu sadələşdirə bilər.
2. Kiçik layihələrdə və ya test məqsədləri üçün qlobal dəyişənlərdən istifadə etmək daha rahat ola bilər.

Lakin, ümumiyyətlə, qlobal dəyişənlərdən istifadə etməkdən çəkinmək və əvəzinə obyekt yönlü proqramlaşdırmanın prinsiplərinə uyğun olaraq məlumatları metodlar arasında ötürmək tövsiyə olunur.

Insertion Sort sadə və asan başa düşülən sıralama alqoritmlərindən biridir. Bu alqoritm son sıralanmış massivi bir elementi digərinin ardınca yerbəyer etməklə qurur. Quicksort, Heapsort və Merge Sort kimi daha mürəkkəb alqoritmlərlə müqayisədə böyük listlərdə daha az effektivdir. Lakin bəzi üstünlüklərə malikdir:

1. Sadədir – asan başa düşülür və tətbiq edilir.
2. Kiçik və demək olar ki, sıralanmış listlərdə yaxşı performans göstərir.
3. Yerində sıralama (in-place sort) alqoritmidir, yəni əlavə yaddaş tələb etmir.

Bu alqoritmin zaman mürəkkəbliyi:

• Ən pis və orta hallarda: O(n²)
• Ən yaxşı halda (əgər massiv artıq sıralanıbsa): O(n)

İnsertion Sort-un işləmə mexanizmi

1. Xarici dövrü (outer loop) başlat – i = 1-dən başlayaraq massiv sonuna qədər iterasiya et.
2. İki dəyişən müəyyən et:
   • current – cari elementin (arr[i]) dəyərini saxlayır.
   • j – i-1 dəyərinə bərabər olan indeksdir.
3. Daxili while dövrü başlat və aşağıdakı şərtləri yoxla:
   • j >= 0 olduqda və
   • arr[j] current-dən böyük olduqda.
4. Əgər şərt ödənirsə:
   • arr[j+1] = arr[j] – yəni j indeksində olan elementi sağa ötür.
   • j dəyərini bir vahid azaldır.
5. Xarici dövrün sonunda arr[j+1] current dəyərinə bərabər edilir.
6. Sonda sıralanmış massivi qaytarır.

Həlli (JavaScript)

const insertionSort = (arr) => {
  for (let i = 1; i < arr.length; i++) {
    let currentElement = arr[i];
    let j = i - 1;

    while (j >= 0 && arr[j] > currentElement) {
      arr[j + 1] = arr[j];
      j--;
    }

    arr[j + 1] = currentElement;
  }

  return arr;
}

Bu funksiya yerində (in-place) sıralama aparır və əlavə yaddaş istifadə etmir. Kiçik massivlər üçün ideal seçimdir.

Video izahı (ingiliscə)

Vizual izahı

Əgər sadə, asan başa düşülən və kiçik massivlər üçün effektiv bir sıralama alqoritmi axtarırsınızsa, Insertion Sort yaxşı seçim ola bilər. Lakin böyük massivlər üçün Quicksort və Merge Sort kimi daha optimallaşdırılmış alqoritmlər tövsiyə olunur.

Java proqramlaşdırma dilində məlumatların saxlanması və idarə olunması üçün həm massivlər (array), həm də ArrayList-lər geniş istifadə olunur. Hər iki strukturun özünəməxsus xüsusiyyətləri, üstünlükləri və çatışmazlıqları mövcuddur. Bu məqalədə, massivlər və ArrayList-lər arasındakı fərqləri, onların istifadəsini və hansı hallarda daha uyğun olduqlarını araşdıracağıq.

Massivlər (Array)

Massivlər eyni tipli məlumatların sabit ölçülü kolleksiyasını saxlamaq üçün istifadə olunan fundamental məlumat strukturudur. Massivin ölçüsü yaradılarkən təyin edilir və sonradan dəyişdirilə bilməz.

Xüsusiyyətləri:

• Sabit Ölçü: Massivin ölçüsü yaradılarkən müəyyən edilir və sonradan dəyişdirilə bilməz.
• Sürətli Məlumat Əldəetmə: İndeks əsasında məlumatlara sürətli giriş imkanı verir.
• Primitiv və Obyekt Tipləri: Massivlər həm primitiv tipləri (məsələn, int, double), həm də obyektləri saxlaya bilər.

Nümunə:

int[] numbers = new int[3];
numbers[0] = 5;
numbers[1] = 10;
numbers[2] = 15;
System.out.println(numbers[0]); // 5

Çatışmazlıqları:

• Ölçünün Dəyişdirilə Bilməməsi: Massivin ölçüsü sabit olduğundan, əlavə elementlər əlavə etmək üçün yeni bir massiv yaratmaq və mövcud elementləri köçürmək lazımdır.
• Metodların Məhdudluğu: Massivlərdə yalnız əsas əməliyyatlar mövcuddur və əlavə funksionallıq üçün əl ilə kod yazmaq tələb olunur.

ArrayList

ArrayList, Java Collections Framework-ün bir hissəsi olan və dinamik ölçülü massivləri təqlid edən bir classdır. Elementlərin sayına uyğun olaraq avtomatik genişlənə və ya kiçilə bilər.

Xüsusiyyətləri:

• Dinamik Ölçü: Elementlərin sayına uyğun olaraq ölçüsü avtomatik tənzimlənir.
• Metodların Çeşidliliyi: Element əlavə etmək, silmək, axtarmaq və digər əməliyyatlar üçün zəngin metodlar toplusu təqdim edir.
• Yalnız Obyekt Tipləri: ArrayList yalnız obyektləri saxlaya bilər; primitiv tiplər üçün müvafiq wrapper classlardan (məsələn, int əvəzinə Integer) istifadə etmək lazımdır.

Nümunə:

import java.util.ArrayList;

public class Example {
    public static void main(String[] args) {
        ArrayList<String> fruits = new ArrayList<>();
        fruits.add("Alma");
        fruits.add("Armud");
        fruits.add("Şaftalı");
        System.out.println(fruits.get(0)); // "Alma"
    }
}

Üstünlükləri:

• Ölçünün Elastikliyi: Elementlərin sayına uyğun olaraq ölçü avtomatik tənzimlənir, bu da proqramın daha çevik olmasını təmin edir.
• Zəngin Metodlar: Elementlərin idarə olunması üçün müxtəlif metodlar təqdim edir, bu da kodun yazılmasını asanlaşdırır.

Çatışmazlıqları:

• Performans: Bəzi hallarda, xüsusilə böyük həcmli məlumatlarla işləyərkən, ArrayList-lərin performansı massivlərə nisbətən daha aşağı ola bilər.
• Yaddaş İstifadəsi: ArrayList-lər əlavə yaddaş sərfiyyatına səbəb ola bilər, çünki onların ölçüsü dinamik olaraq dəyişir və bu, əlavə yaddaş ayırmalarına gətirib çıxara bilər.

Massiv və ArrayList Arasındakı Fərqlər

Hansı hallarda hansını seçmək lazımdır?

• Massivlər: Əgər məlumatların sayı əvvəlcədən məlumdursa və sabitdirsə, həmçinin yüksək performans tələb olunursa, massivlər daha uyğun seçimdir.
• ArrayList-lər: Məlumatların sayı dinamik olaraq dəyişirsə və əlavə metodların funksionallığına ehtiyac varsa, ArrayList-lər daha uyğun seçimdir.

AzePUG-dan möhtəşəm izahı. Düşünürəm bundan daha geniş izahını tapmaq çətin olar.

Data_Structures_Algo_Python/book/3.Birtərəfli_Əlaqəli_listlər_singly_linked_lists.md at master · AzePUG/Data_Structures_Algo_Python

Azərbaycan dilində "Data strukturları və Alqoritmlər" mövzusunda Open Source kitab. - Data_Structures_Algo_Python/book/3.Birtərəfli_Əlaqəli_listlər_singly_linked_lists.md at master · AzePUG/Data_Structures_Algo_Python

GitHub (github.com)

Tək istiqamətli əlaqəli listlər (Singly Linked List), hər elementi iki hissədən ibarət olan düyünlərdən (node) ibarət olan məlumat strukturudur: dəyər (data) və növbəti düyünə keçid (next pointer). Siyahının sonuncu düyünü null-a bərabər olur ki, bu da siyahının sonlandığını bildirir.

Bu məlumat strukturunun əsas məqsədi dinamik element kolleksiyasını səmərəli şəkildə saxlamaq və idarə etməkdir. Tək istiqamətli listlərin ən böyük üstünlüyü başlanğıc və ortada yerləşdirmə və silmə əməliyyatlarını effektiv şəkildə yerinə yetirməkdir. Bunun səbəbi odur ki, bu əməliyyatlar sadece bir neçə göstəricinin (pointer) dəyişdirilməsi ilə həyata keçirilir, bu da massivlərə (arrays) nisbətən daha səmərəli bir həll təqdim edir.

Linked Listlərin Üstünlükləri və Çatışmazlıqları

Linked Listdən real həyatda istifadə halları

1. Musiqi Pleylistləri - Hər bir mahnı bir düyün kimi saxlanılır və növbəti mahnıya keçid mövcuddur.
2. Brauzer Tarixi - Brauzerlər istifadəçilərin gəzdiyi səhifələri bağlı siyahı şəklində saxlayır.
3. Tapşırıq Siyahıları (Task List) - Tapşırıqlar asanlıqla əlavə və silinə bilir.
4. Undo/Redo Funksionallığı - Bağlı siyahılar istifadəçilərin etdiyi dəyişiklikləri geri qaytarmaq üçün istifadə olunur.
5. Fayl Sistemləri - Faylların və qovluqların idarə olunmasında tək istiqamətli bağlı siyahılardan istifadə edilə bilər.
6. Simvol Cədvəlləri (Symbol Tables) - Proqramlaşdırma dillərinin kompilyatorlarında istifadə olunur.
7. Növbə Strukturları (Queue Data Structures) - İşlənəcək elementlərin idarə edilməsi üçün sıralama strukturu olaraq tətbiq edilir.
8. GPS Naviqasiya Sistemləri - İstiqamət və marşrutların saxlanması üçün bağlı siyahılardan istifadə olunur.
9. Log Faylları - Sistem hadisələri bağlı siyahılar şəklində saxlanıla bilər.
10. Sosial Media Lentləri - Postlar tək istiqamətli bağlı siyahı şəklində saxlanılır.
11. Şəbəkə Paket Növbələri - Şəbəkə protokolları paketin ötürülməsini bağlı siyahı kimi idarə edə bilər.
12. Versiya Nəzarət Sistemləri (Git) - Hər bir commit bir düyün kimi saxlanılır.

JavaScript-də tək istiqamətli əlaqəli listlərin implementasiyası

Əsas classlar (Base Classes)

• Node classı hər bir düyünün dəyərini və növbəti düyünə keçidi saxlayır.
• LinkedList classı isə siyahını idarə etmək üçün istifadə olunur.

class Node {
    constructor(value) {
        this.val = value;
        this.next = null;
    }
}

class LinkedList {
    constructor() {
        this.head = null;
        this.tail = null;
        this.length = 0;
    }
}

Siyahıya əlavə (Push) - O(1)

push(value) {
    const newNode = new Node(value);

    if (!this.head) {
        this.head = newNode;
    } else {
        this.tail.next = newNode;
    }

    this.tail = newNode;
    this.length++;
    return this;
}

Sonuncu düyünü silmə (Pop) - O(n)

pop() {
    if (!this.length) return undefined;

    let current = this.head;
    let newTail = current;

    while (current.next) {
        newTail = current;
        current = current.next;
    }

    this.tail = newTail;
    this.tail.next = null;
    this.length--;

    return current;
}

Başlanğıcdan silmə (Shift) - O(1)

shift() {
    if (!this.length) return undefined;

    let current = this.head;
    this.head = current.next;
    this.length--;

    return current;
}

Başlanğıca əlavə (Unshift) - O(1)

unshift(value) {
    const newNode = new Node(value);

    if (!this.head) {
        this.head = newNode;
        this.tail = newNode;
    } else {
        newNode.next = this.head;
        this.head = newNode;
    }

    this.length++;
    return this;
}

Verilən düyünü tapmaq (Get) - O(n)

get(index) {
    if (index < 0 || index >= this.length) return null;

    let current = this.head;
    let counter = 0;

    while (counter !== index) {
        current = current.next;
        counter++;
    }

    return current;
}

Düyünün dəyərini dəyişmək (Set) - O(n)

set(value, index) {
    const foundNode = this.get(index);
    if (!foundNode) return false;

    foundNode.val = value;
    return true;
}

Siyahını tərsinə çevirmək (Reverse) - O(n)

reverse() {
    let node = this.head;
    this.head = this.tail;
    this.tail = node;

    let prev = null;
    let next;

    while (node) {
        next = node.next;
        node.next = prev;
        prev = node;
        node = next;
    }

    return this;
}

Bu yazıda Tək istiqamətli əlaqəli listlərin (Singly Linked List) əsaslarını, üstünlüklərini, istifadələrini və JavaScript-də implementasiyasını öyrəndik. Bu mövzunu daha dərindən başa düşmək üçün fərqli alqoritmlərlə test etmək və real layihələrdə tətbiq etmək tövsiyə olunur.

Azerbaijan Python User Group-dan Şəhriyar abimizin Stack-la bağlı paylaşdığı gözəl yazısı.

Data_Structures_Algo_Python/book/6.Stack_Yığın.md at master · AzePUG/Data_Structures_Algo_Python

Azərbaycan dilində "Data strukturları və Alqoritmlər" mövzusunda Open Source kitab. - Data_Structures_Algo_Python/book/6.Stack_Yığın.md at master · AzePUG/Data_Structures_Algo_Python

GitHub (github.com)

Ağac (Tree) verilənlər strukturu iyerarxik düyünlər (nodes) kolleksiyasıdır. Hər bir düyünün bir dəyəri olur və sıfır və ya daha çox alt düyünlərə (child nodes) sahib ola bilər. Ağaclar fayl sistemlərində, təşkilati diaqramlarda, verilənlərin axtarışı və sıralanması kimi sahələrdə geniş istifadə olunur. Ağacın yuxarı hissəsində kök (root) düyünü yerləşir, ondan aşağıya doğru budaqlanan düyünlər isə ən aşağı səviyyədə yarpaq (leaf) düyünləri ilə tamamlanır.

Ağac Terminologiyası

• Kök (Root) - Ağacın ən üst düyünü;
• Uşaq (Child) - Birbaşa başqa bir düyünə bağlı olan düyün;
• Valideyn (Parent) - Uşaq düyününə birbaşa bağlı olan düyün;
• Bacı-qardaş (Siblings) - Eyni valideynə sahib olan düyünlər;
• Yarpaq (Leaf) - Uşaq düyünü olmayan düyün;
• Kənar (Edge) - İki düyün arasındakı əlaqə.

İkili axtarış ağacı (BST) necə işləyir?

İkili axtarış ağacı (Binary Search Tree, BST) xüsusi bir ağac növüdür. Burada:

• Hər bir valideyn düyünü maksimum iki uşaq düyünə sahib ola bilər;
• Sol tərəfdəki bütün düyünlər həmişə valideyn düyünündən kiçik olur;
• Sağ tərəfdəki bütün düyünlər həmişə valideyn düyünündən böyük olur.

Bu struktur məlumatların səmərəli axtarışı və idarə olunması üçün idealdır.

BST-in implementasiyası

1. Əsas classın yaradılması

BST yaratmaq üçün aşağıdakı addımları yerinə yetiririk:

1. BinarySearchTree adlı class yaradılır və constructor-da this.root = null təyin olunur.
2. Node adlı class yaradılır. Bu class:
   • value parametrini qəbul edir və this.value-a təyin edir;
   • this.left və this.right sahələri null olaraq başlayır.

2. Düyünün ağaca əlavə edilməsi (Insert metodu)

BST-də yeni düyün əlavə etmək üçün:

1. Yeni düyün yaradılır.
2. Əgər ağac boşdursa, yeni düyün root olur.
3. Əgər root varsa:
   • Əgər yeni düyünün dəyəri root-dan kiçikdirsə, sol tərəfə yerləşdirilir.
   • Əgər root-dan böyükdürsə, sağ tərəfə yerləşdirilir.
4. Əgər uyğun mövqe tapılmazsa, düyün rekursiv şəkildə yerləşdirilir.

Kod nümunəsi:

insert(value) {
  const newNode = new Node(value);

  if (!this.root) {
    this.root = newNode;
    return this;
  }

  let current = this.root;
  while (true) {
    if (value === current.value) return undefined;
    
    const direction = value < current.value ? 'left' : 'right';
    if (!current[direction]) {
      current[direction] = newNode;
      return this;
    } else {
      current = current[direction];
    }
  }
}

3. Axtarış funksiyası (Find metodu)

Düyünün ağacda olub-olmadığını yoxlamaq üçün:

1. root yoxlanılır. Əgər root boşdursa, axtarış dayandırılır.
2. Əgər root-un dəyəri axtarılan dəyərə bərabərdirsə, düyün tapıldı.
3. Əgər axtarılan dəyər root-dan kiçikdirsə, sol budaqda axtarış davam edir.
4. Əgər axtarılan dəyər root-dan böyükdürsə, sağ budaqda axtarış davam edir.

Kod nümunəsi:

find(value) {
  if (!this.root) return false;
  let current = this.root;
  while (current) {
    if (value < current.value) {
      current = current.left;
    } else if (value > current.value) {
      current = current.right;
    } else {
      return current;
    }
  }
  return false;
}

İkili Ağacda axtarış alqoritmləri

Ağaclarda iki əsas axtarış metodu var:

1. BFS (Eninə Axtarış - Breadth-First Search)
2. DFS (Dərinliyə Axtarış - Depth-First Search)

1. BFS (Breadth-First Search) – Eninə Axtarış

BFS metodunda axtarış səviyyə-səviyyə aparılır:

1. Queue strukturu yaradılır.
2. Kök düyünü queue-yə əlavə edilir.
3. Queue boş olmadığı müddətcə:
   • Queue-dən düyün çıxarılır.
   • Onun sol və sağ düyünləri queue-yə əlavə edilir.
4. Axtarış başa çatır və nəticə qaytarılır.

Kod nümunəsi:

BFS() {
  let node = this.root,
    data = [],
    queue = [];

  queue.push(node);

  while (queue.length) {
    node = queue.shift();
    data.push(node.value);
    if (node.left) queue.push(node.left);
    if (node.right) queue.push(node.right);
  }

  return data;
}

2. DFS (Depth-First Search) – Dərinliyə Axtarış

DFS metodunda budaqlar tam araşdırılır və sonra geri qayıdılır.

DFS PreOrder (Öncə Valideyn, Sonra Uşaqlar)

1. Kök düyün data massivinə əlavə edilir.
2. Sol alt ağac ziyarət olunur.
3. Sağ alt ağac ziyarət olunur.

DFSPreOrder(){
  const data = [];

  function traverse(node){
    data.push(node.value);
    if(node.left) traverse(node.left);
    if(node.right) traverse(node.right);
  }

  traverse(this.root);
  return data;
}

DFS PostOrder (Öncə uşaqlar, Sonra valideyn)

1. Sol alt ağac ziyarət olunur.
2. Sağ alt ağac ziyarət olunur.
3. Valideyn düyün data massivinə əlavə edilir.

DFSPostOrder(){
  var data = [];

  function traverse(node){
    if(node.left) traverse(node.left);
    if(node.right) traverse(node.right);
    data.push(node.value);
  }

  traverse(this.root);
  return data;
}

DFS InOrder (Sol -> Valideyn -> Sağ)

1. Sol alt ağac ziyarət olunur.
2. Valideyn düyün data massivinə əlavə edilir.
3. Sağ alt ağac ziyarət olunur.

DFSInOrder(){
  var data = [];

  function traverse(node){
    if(node.left) traverse(node.left);
    data.push(node.value);
    if(node.right) traverse(node.right);
  }

  traverse(this.root);
  return data;
}

Bu məqalədə İkili Axtarış Ağacı (BST) və onun əsas axtarış alqoritmləri haqqında məlumat verdik. BST verilənlərin səmərəli idarə olunması və axtarışı üçün ideal bir strukturdur.

Binary Heap nədir?

Binary Heap, xüsusi ikili ağac (binary tree) əsaslı məlumat strukturu olub, yığın (heap) xüsusiyyətini təmin edir.

Bu struktura görə, hər bir “x” düyünü öz valideyni “p” ilə əlaqəlidir və:

• Max Heap-də valideynin dəyəri hər zaman uşaqlarından böyükdür.
• Min Heap-də valideynin dəyəri hər zaman uşaqlarından kiçikdir.

Binary Heap-in istifadə sahələri

Binary Heap, prioritet növbələri (priority queues) yaratmaq üçün geniş istifadə edilir. Bu strukturlar:
Heap Sort (yığın çeşidləmə) alqoritmində,
Dijkstra və digər qraf alqoritmlərində,
Maksimum və minimum dəyərin sürətli çıxarılması üçün istifadə olunur.

Binary Heap növləri

1. Max Heap:

   • Hər bir valideyn düyünün dəyəri uşaqlarından böyükdür.
   • Ən böyük element həmişə kökdə olur.

2. Min Heap:

   • Hər bir valideyn düyünün dəyəri uşaqlarından kiçikdir.
   • Ən kiçik element həmişə kökdə olur.

Max Binary Heap-in qaydaları

1. Hər valideyn maksimum iki uşaq düyünə sahib ola bilər.
2. Valideynin dəyəri uşaqlarından böyükdür.
3. Qardaş düyünlər arasında heç bir dəyər qaydası yoxdur.
4. Yığın mümkün qədər sıx yerləşdirilir – sol tərəf həmişə ilk doldurulur.

Binary Heap-in JavaScript-də implementasiyası

Binary Heap classın yaradılması

Əsas classı yaradıb, values adlı boş array içində saxlayırıq.

class BinaryHeap {
  constructor() {
    this.values = [];
  }
}

Element əlavə etmə (Insert)

Yeni element daxil etmək üçün insert() metodunu qururuq.

İş prinsipi:

1. Yeni element values array-ə push olunur.
2. Yeni əlavə edilən element “Bubble Up” alqoritmi ilə doğru mövqeyə yerləşdirilir:
   • Yeni elementin indeksi (index) təyin edilir.
   • Valideynin indeksi (parentIndex) hesablanır:
     $$ \text{parentIndex} = \lfloor \frac{index-1}{2} \rfloor $$
   • Valideyn daha kiçikdirsə, yerləri dəyişdirilir (swap edilir) və proses təkrarlanır.

Kod:

insert(element){
  this.values.push(element);
  
  let idx = this.values.length - 1;
  const el = this.values[idx];
  
  while(idx > 0) {
    let parentIdx = Math.floor((idx - 1) / 2);
    let parent = this.values[parentIdx];
    if(el <= parent) break;

    this.values[parentIdx] = el;
    this.values[idx] = parent;
    idx = parentIdx;
  }
}

Element silmə (ExtractMax)

Ən böyük elementi (Max Heap-də) silmək üçün extractMax() metodu yaradılır.

İş Prinsipi:

1. İlk element (ən böyük dəyər) ilə sonuncu element swap edilir.
2. Sonuncu element array-dən silinir (pop edilir).
3. Yeni kök elementi “Sink Down” metodu ilə düzgün mövqeyə yerləşdirilir:
   • Sol və sağ uşaqların indeksləri təyin edilir:
     • leftChildIdx = 2 * index + 1
     • rightChildIdx = 2 * index + 2
   • Əgər hər iki uşaq daha böyükdürsə, ən böyüyü ilə swap edilir.
   • Proses uşaqlardan biri daha böyük olana qədər təkrarlanır.

Kod:

extractMax() {
  const max = this.values[0];
  const end = this.values.pop();

  if (this.values.length > 0) {
    this.values[0] = end;
    let idx = 0;
    const length = this.values.length;
    const element = this.values[0];

    while (true) {
      let leftChildIdx = 2 * idx + 1;
      let rightChildIdx = 2 * idx + 2;
      let leftChild, rightChild;
      let swap = null;

      if (leftChildIdx < length) {
        leftChild = this.values[leftChildIdx];
        if (leftChild > element) {
          swap = leftChildIdx;
        }
      }

      if (rightChildIdx < length) {
        rightChild = this.values[rightChildIdx];
        if (
          (swap === null && rightChild > element) ||
          (swap !== null && rightChild > leftChild)
        ) {
          swap = rightChildIdx;
        }
      }

      if (swap === null) break;

      this.values[idx] = this.values[swap];
      this.values[swap] = element;
      idx = swap;
    }
  }

  return max;
}

Prioritet növbələri (Priority Queue)

Prioritet növbəsi, elementlərin önəmlilik səviyyəsinə görə sıralandığı məlumat strukturudur.

İş prinsipi:

• Kiçik dəyər daha yüksək prioritet deməkdir.
• Enqueue (Daxil Etmə): Yeni düyün priority-ə görə yerləşdirilir.
• Dequeue (Sil və Qaytar): Kök elementi çıxarır və yığını yenidən tənzimləyir.

Prioritet növbəsinin JavaScript-də implementasiyası

class PriorityQueue {
  constructor() {
    this.values = [];
  }

  enqueue(val, priority) {
    let newNode = new Node(val, priority);
    this.values.push(newNode);
    this.bubbleUp();
  }

  bubbleUp() {
    let idx = this.values.length - 1;
    const element = this.values[idx];
    while (idx > 0) {
      let parentIdx = Math.floor((idx - 1) / 2);
      let parent = this.values[parentIdx];
      if (element.priority >= parent.priority) break;
      this.values[parentIdx] = element;
      this.values[idx] = parent;
      idx = parentIdx;
    }
  }

  dequeue() {
    const min = this.values[0];
    const end = this.values.pop();
    if (this.values.length > 0) {
      this.values[0] = end;
      this.sinkDown();
    }
    return min;
  }
}

Node classı:

class Node {
  constructor(val, priority) {
    this.val = val;
    this.priority = priority;
  }
}

İstifadə nümunəsi:

let ER = new PriorityQueue();
ER.enqueue("common cold", 5);
ER.enqueue("gunshot wound", 1);
ER.enqueue("high fever", 4);
ER.enqueue("broken arm", 2);
ER.enqueue("glass in foot", 3);
ER.enqueue("grenade wound", 1);

console.log(ER);
console.log("***************");
console.log(ER.dequeue());

Nəticə

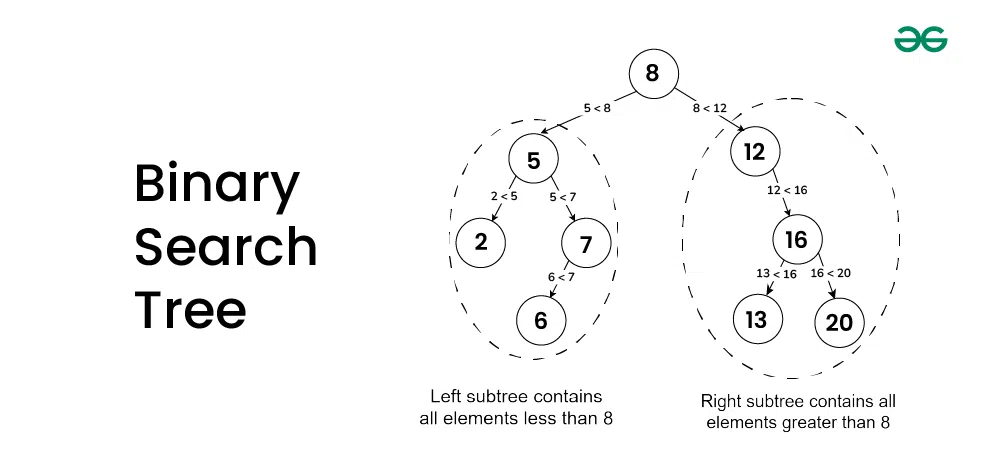
Binary Heap, Max Heap və Min Heap olaraq iki növə ayrılır.
Prioritet növbələri Binary Heap üzərində qurula bilər.
Heap əsaslı alqoritmlər qraf alqoritmlərində və çeşidləmədə geniş istifadə olunur.

Graph nədir?

Graph (Qraf) — düyünlərdən (vertex) və onları birləşdirən kənarlardan (edge) ibarət olan bir məlumat strukturudur. Kənarlar iki düyün arasındakı əlaqəni təmsil edir.

Qraflar çoxşaxəli və geniş istifadə edilən məlumat strukturlarıdır. Onlar sosial şəbəkələr, nəqliyyat şəbəkələri, yol xəritələri və daha çox real dünya sistemlərinin modelləşdirilməsi üçün istifadə edilir.

Qraf növləri:

• İstiqamətli (Directed) və istiqamətsiz (Undirected) qraflar;
• Çəkili (Weighted) və çəkisiz (Unweighted) qraflar;
• Dövrəli (Cyclic) və dövrəsiz (Acyclic) qraflar.

Qraf alqoritmləri qoşulma (connectivity), ən qısa yol (shortest path), keçidlər (traversals) kimi problemləri həll etmək üçün vacibdir.

Əsas Qraf terminləri

Qrafın JavaScript-də implementasiyası

Qrafı obyektlər və siyahılar vasitəsilə təmsil edə bilərik. Burada “Adjacency List” (Qonşuluq Siyahısı) istifadə edəcəyik.

class Graph {
  constructor() {
    this.adjacencyList = {};
  }
}

Vertex (Düyün) əlavə etmə

Yeni bir düyün (vertex) əlavə etmək üçün addVertex() metodunu yaradırıq.

Addım-addım izah:

1. addVertex metodu vertex adında bir parametr qəbul edir.
2. Əgər həmin vertex adjacency list-də yoxdursa, yeni açar (key) kimi əlavə edilir.
3. Əlavə edilən vertex-in dəyəri boş array olur (çünki hələ əlaqəsi yoxdur).

Kod:

addVertex(vertex) {
  if (!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}

Edge (Kənar) əlavə etmə

İki düyün arasında əlaqə (kənar) yaratmaq üçün addEdge() metodunu yaradırıq.

Addım-addım izah:

1. Metod iki vertex qəbul edir (v1 və v2).
2. v1 açarını tapıb, onun array-nin içinə v2-ni əlavə edirik.
3. v2 açarını tapıb, onun array-nin içinə v1-i əlavə edirik.
4. Bununla, hər iki vertex bir-birinə bağlı olur.

Kod:

addEdge(v1, v2) {
  this.adjacencyList[v1].push(v2);
  this.adjacencyList[v2].push(v1);
}

Edge (Kənar) silmə

İki düyün arasındakı əlaqəni silmək üçün removeEdge() metodunu yaradırıq.

Addım-addım izah:

1. Metod iki vertex qəbul edir (v1 və v2).
2. v1 açarına baxırıq və v2-ni siyahıdan çıxarırıq.
3. v2 açarına baxırıq və v1-i siyahıdan çıxarırıq.

Kod:

removeEdge(v1, v2) {
  this.adjacencyList[v1] = this.adjacencyList[v1].filter(
    v => v !== v2
  );

  this.adjacencyList[v2] = this.adjacencyList[v2].filter(
    v => v !== v1
  );
}

Vertex (Düyün) silmə

Bütün əlaqələri ilə birlikdə bir vertex silmək üçün removeVertex() metodunu yaradırıq.

Addım-addım izah:

1. Metod silinməsi lazım olan vertex qəbul edir.
2. Həmin vertex-in qonşuluq siyahısı boşalana qədər onun hər bir əlaqəsini removeEdge() funksiyası ilə silirik.
3. Sonda vertex-i adjacency list-dən tamamilə silirik.

Kod:

removeVertex(vertex) {
  while (this.adjacencyList[vertex].length) {
    const adjacentVertex = this.adjacencyList[vertex].pop();
    this.removeEdge(vertex, adjacentVertex);
  }
  delete this.adjacencyList[vertex];
}

Nəticə

• Qraf məlumat strukturu düyünlər və onları birləşdirən kənarlardan ibarətdir.
• İstiqamətli, istiqamətsiz, çəkili və çəkisiz qraf tipləri mövcuddur.
• Adjacency List (Qonşuluq Siyahısı) qrafı təmsil etmək üçün effektiv üsuldur.
• Vertex əlavə etmə, edge əlavə etmə, edge silmə və vertex silmə əməliyyatlarını JavaScript ilə tətbiq etdik.

Qraflar geniş istifadə edilən bir məlumat strukturu olub, şəbəkələr, yol tapma alqoritmləri, sosial platformalar və daha çox sahədə tətbiq edilir.

mycodeschool Graph-ları çox rahat formada izah edir. Baxmağa dəyər.

Queue nədir?

Queue (növbə) — First-In-First-Out (FIFO - İlk Daxil Olan İlk Çıxır) prinsipi ilə işləyən bir məlumat strukturudur. Queue-da elementlər sona əlavə edilir və ön hissədən çıxarılır.

Queue aşağıdakı sahələrdə geniş istifadə olunur:

• Arxa planda işləyən proseslər (məsələn, mesaj sistemləri);
• Resursların yüklənməsi (məsələn, şəkil və ya fayl yükləmə növbələri);
• Onlayn oyunlarda oyunçuların növbəyə salınması;
• Çap və tapşırıqların emalı (məsələn, printer növbələri).

Queue-in JavaScript-də implementasiyası

Queue üçün əsas class-lar

Queue yaratmaq üçün əvvəlcə Node və Queue classlarını müəyyən etməliyik.

Node classı:

• Constructor qəbul etdiyi value parametrini this.value-ə mənimsədir;
• this.next default olaraq null olur.

Queue classı:

• Constructor heç bir parametr qəbul etmir, amma this.first və this.last dəyərləri null olur;
• this.size dəyişəni isə 0-dır.

class Node {
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

class Queue {
  constructor() {
    this.first = null;
    this.last = null;
    this.size = 0;
  }
}

Element əlavə etmə (Enqueue) — O(1)

Queue-ya sona element əlavə etmək üçün enqueue() metodunu yazırıq.

Addım-addım izah:

1. Yeni bir Node yaradırıq və ona dəyər ötürürük.
2. Əgər queue boşdursa, first və last propertiləri bu yeni node-a bərabər olur.
3. Əks halda, mövcud last-ın next propertiyini yeni node-a yönəldirik.
4. last propertiyini bu yeni node kimi təyin edirik.
5. Queue-nin ölçüsünü (size) artırırıq və qaytarırıq.

Kod:

enqueue(value) {
  const newNode = new Node(value);

  if (!this.first) {
    this.first = newNode;
    this.last = newNode;
  } else {
    this.last.next = newNode;
    this.last = newNode;
  }

  return ++this.size;
}

Element silmə (Dequeue) — O(1)

Queue-dan başdan element silmək üçün dequeue() metodunu yazırıq.

Addım-addım izah:

1. Əgər queue boşdursa (this.first === null), null qaytarırıq.
2. Mövcud first dəyərini müvəqqəti (temp) dəyişəndə saxlayırıq.
3. Əgər queue-da tək element varsa (first === last), last-ı null edirik.
4. First dəyərini this.first.next-ə təyin edirik.
5. Queue-nin ölçüsünü (size) azaldırıq və silinmiş elementin (temp) dəyərini qaytarırıq.

Kod:

dequeue() {
  if (!this.first) return null;
  
  const temp = this.first;
  
  if (this.first === this.last) {
    this.last = null;
  }

  this.first = this.first.next;
  this.size--;

  return temp.value;
}

Nəticə

Queue FIFO prinsipi ilə işləyən bir məlumat strukturudur və proqramlaşdırmada geniş istifadə olunur. Element əlavə etmə və silmə əməliyyatları O(1) vaxt mürəkkəbliyinə malikdir.

Bu məqalədə Queue-in JavaScript-də necə qurulmasını və enqueue/dequeue əməliyyatlarının necə həyata keçirildiyini öyrəndik. Queue, xüsusilə resurs yüklənməsi, oyunçuların idarə edilməsi və tapşırıqların emalı kimi sahələrdə geniş istifadə edilir.

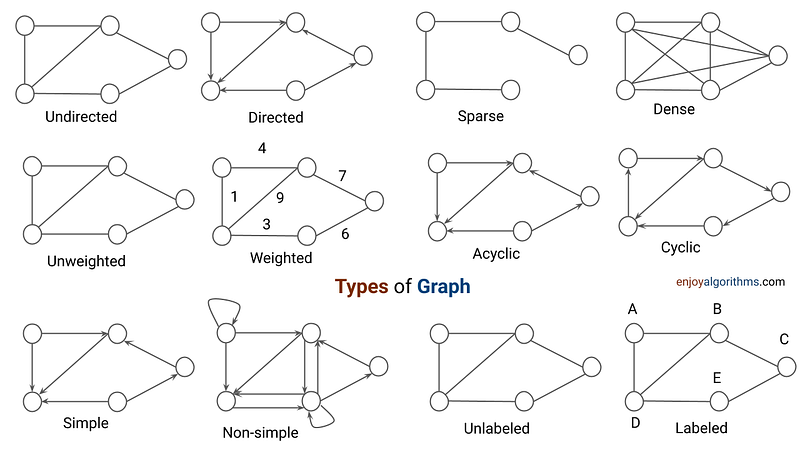
Vue-da dinamik hadisə adlarından istifadə edə biləcəyinizi bilirdinizmi? Hadisə dinləyicilərini “hard code” əvəzinə, onları hesablanmış hadisə adları ilə v-on (@) istifadə edərək dinamik şəkildə bağlaya bilərsiniz:

<script setup lang="ts">
import { computed, ref } from 'vue';

const event = ref<'mouseover' | 'click'>('mouseover');

const eventHistory = ref<Array<string>>([]);

const buttonLabel = computed(() =>
  event.value === 'mouseover' ? 'Hover Me' : 'Click Me'
);

const onHandleEvent = () => {
  eventHistory.value = [
    ...eventHistory.value,
    `${new Date().toISOString()}: ${event.value}`,
  ];
};
</script>

<template>
  <div class="wrapper">
    <div class="wrapper">
      <span>Select an event type: </span>
      <div>
        <label>
          <input type="radio" name="event" v-model="event" value="mouseover" />
          On Hover
        </label>

        <label>
          <input type="radio" name="event" v-model="event" value="click" />
          On Click
        </label>
      </div>
    </div>
    <button @[event]="onHandleEvent">{{ buttonLabel }}</button>
    <div class="wrapper" v-if="eventHistory.length > 0">
      <strong>Event History:</strong>
      <span v-for="entry of eventHistory">{{ entry }}</span>
    </div>
  </div>
</template>

<style scoped>
.wrapper {
  display: flex;
  flex-direction: column;
  gap: 5px;
}
</style>

Demo

Vue Tip: Dynamic Event Names - StackBlitz

Next generation frontend tooling. It's fast!

StackBlitz (stackblitz.com)