Generics — TypeScript-də məlumatların tipini dinamik şəkildə müəyyən etmək üçün istifadə olunan bir vasitədir. Generics proqramlarımızı yenidən istifadə edilə bilən və tip təhlükəsizliyi təmin edən şəkildə yazmağımıza kömək edir.
Bu konsept bizə funksiyalarda, interfeyslərdə, classlarda və tiplərdə konkret tip əvəzinə gələcəkdə təyin ediləcək tip dəyişəni (T, U, K, s.) istifadə etməyə imkan verir.
 Niyə Generics istifadə olunur?
Niyə Generics istifadə olunur?
Əgər bir funksiyanı müxtəlif tiplərlə işləyəcək şəkildə yazmaq istəyiriksə və həmçinin TypeScript-in tip yoxlamasından faydalanmaq istəyiriksə, Generics çox faydalıdır.
 Sadə Generics nümunəsi
Sadə Generics nümunəsi
function identity<T>(value: T): T {
return value;
}
const str = identity<string>("Hello");
const num = identity<number>(42);
Bu nümunədə identity funksiyası hər hansı tipdə (T) dəyər alır və onu geri qaytarır. Bu funksiyanı həm string, həm number, həm də başqa istənilən tiplərlə istifadə etmək olar.
 Generics ilə Array işlənməsi
Generics ilə Array işlənməsi
function getFirstElement<T>(arr: T[]): T {
return arr[0];
}
const first = getFirstElement<string>(["apple", "banana"]);
const firstNum = getFirstElement<number>([10, 20, 30]);
Burada T[] generik array-dir. Hansı tipdə array versəniz, TypeScript həmin tipdə cavab qaytaracaq.
 Generics ilə Interface və Type-lar
Generics ilə Interface və Type-lar
interface Box<T> {
content: T;
}
const stringBox: Box<string> = { content: "salam" };
const numberBox: Box<number> = { content: 123 };
Burada Box<T> interfeysi istənilən tipdə məlumat saxlamaq üçün generik olaraq təyin olunub.
 Generics ilə Class
Generics ilə Class
class Container<T> {
private value: T;
constructor(val: T) {
this.value = val;
}
getValue(): T {
return this.value;
}
}
const container = new Container<string>("Data");
console.log(container.getValue()); // "Data"
Bu nümunədə Container class-ı generikdir və istənilən tipdə məlumat saxlaya bilir.
 Bir neçə tip dəyişəni ilə Generics
Bir neçə tip dəyişəni ilə Generics
function merge<T, U>(obj1: T, obj2: U): T & U {
return { ...obj1, ...obj2 };
}
const merged = merge({ name: "Ali" }, { age: 25 });
// merged: { name: "Ali", age: 25 }
merge funksiyası iki fərqli tip qəbul edir və onların birləşməsini qaytarır.
 Tip məhdudiyyətləri (Constraints)
Tip məhdudiyyətləri (Constraints)
Bəzən generik tipin müəyyən xüsusiyyətləri olmasını istəyə bilərik. Bu zaman extends istifadə olunur:
function logLength<T extends { length: number }>(value: T): void {
console.log(value.length);
}
logLength("Salam"); // 5
logLength([1, 2, 3]); // 3
Bu nümunədə T tipi yalnız length xüsusiyyətinə sahib olan tiplərlə məhdudlaşdırılıb.

keyof Operatoru
keyof operatoru bir obyektin açarlarını (key) tip kimi əldə etməyə imkan verir.
interface Person {
name: string;
age: number;
}
type PersonKeys = keyof Person; // "name" | "age"
Bu, xüsusilə dinamik açarlarla işləyərkən faydalıdır:
function getProperty<T, K extends keyof T>(obj: T, key: K): T[K] {
return obj[key];
}
const person = { name: "Ali", age: 30 };
const name = getProperty(person, "name"); // "Ali"

infer və Conditional Types
Conditional types tip əsaslı şərti ifadələr yaratmağa imkan verir. infer isə bu şərtlər daxilində tip çıxarmağa (inference) kömək edir.
infer ilə tip çıxarma
type ReturnType<T> = T extends (...args: any[]) => infer R ? R : any;
type Num = ReturnType<() => number>; // number
type Str = ReturnType<(x: string) => string>; // string
Burada infer R funksiyanın dönüş tipini çıxarır.
Flatten nümunəsi
type Flatten<T> = T extends Array<infer U> ? U : T;
type Str = Flatten<string[]>; // string
type Num = Flatten<number>; // number
Əgər T array tipidirsə, onun element tipini çıxarır, əks halda T-ni olduğu kimi saxlayır.
 Default Generic parametrlər
Default Generic parametrlər
Generik parametrlər üçün default (susmaya görə) dəyərlər təyin etmək mümkündür:
function createArray<T = number>(length: number, value: T): T[] {
return new Array(length).fill(value);
}
const numberArray = createArray(3, 0); // [0, 0, 0]
const stringArray = createArray<string>(3, "hello"); // ["hello", "hello", "hello"]
Burada T üçün default olaraq number tipi təyin edilib.
 Generics-in Üstünlükləri
Generics-in Üstünlükləri
| Üstünlük | İzah |
|---|---|
 Yenidən istifadə Yenidən istifadə |
Eyni funksiya və ya sinif müxtəlif tiplərlə işləyə bilir. |
 Tip təhlükəsizliyi Tip təhlükəsizliyi |
Giriş və çıxış tipləri dəqiq müəyyənləşir. |
 Daha az təkrar kod Daha az təkrar kod |
Eyni əməliyyatı fərqli tiplərlə etmək üçün ayrıca funksiyalara ehtiyac yoxdur. |
 Nəticə
Nəticə
Generics TypeScript-də çox güclü bir vasitədir və proqramların daha elastik, tip təhlükəsiz və yenidən istifadə oluna bilən olmasını təmin edir.
Əgər siz funksiyalarınızın və strukturlarınızın tiplərini gələcəkdə təyin etmək istəyirsinizsə və təkrarı azaltmaq istəyirsinizsə — Generics istifadə etməyiniz tövsiyə olunur.


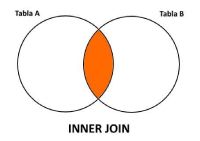
 1.
1. 
 2.
2. 
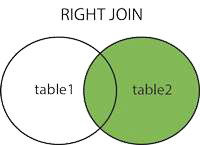
 3.
3. 
 4.
4.  Prototip nədir?
Prototip nədir? Prototip zəncirində dərinlik
Prototip zəncirində dərinlik ️ Diqqət:
️ Diqqət:  2.
2.  ️ 4.
️ 4. 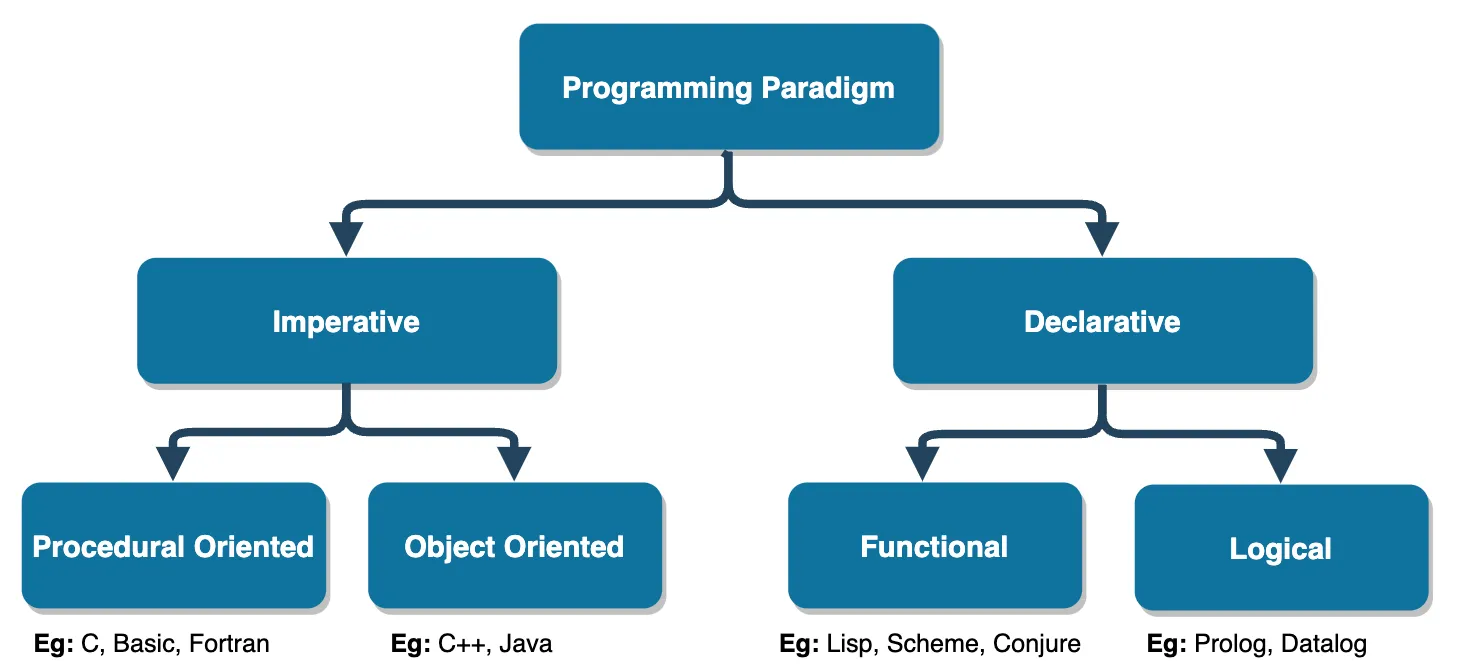
 Əsas proqramlaşdırma paradigmaları
Əsas proqramlaşdırma paradigmaları Nəticə
Nəticə ️
️